x <- seq(-10, 10, by = .1)
curve(dnorm(x, mean = 0, sd = 1), from=-4, to=4)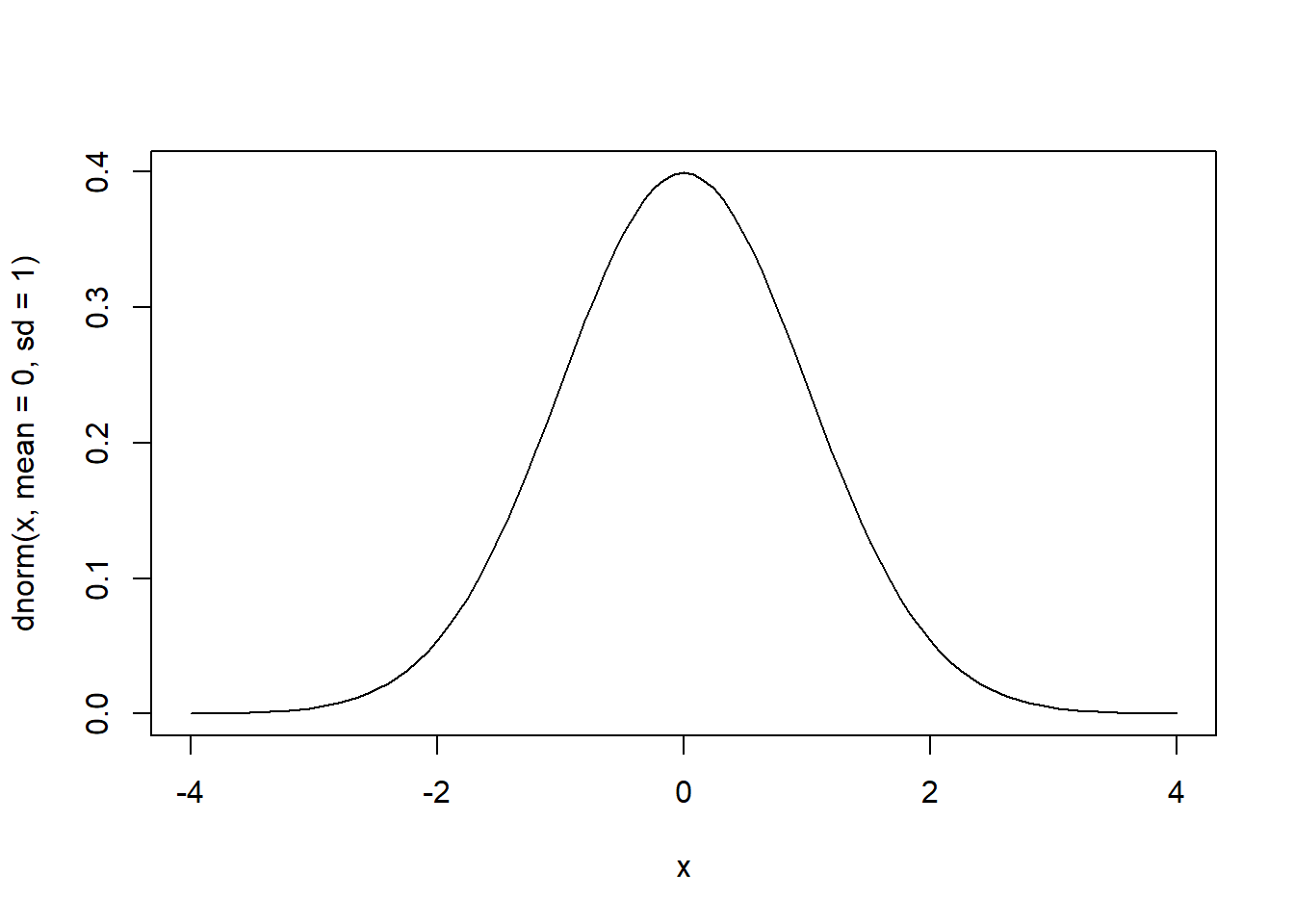
R heeft verschillende ingebouwde functies om de normaalverdeling te gebruiken.
Een ervan is de functie dnorm(). Deze functie geeft de hoogte van de kansverdeling in elk punt voor een gegeven gemiddelde en standaardafwijking. Hiermee kunnen we een normale verdeling specificeren met behulp van drie elementen:
x is een vector van getallen.mean is de gemiddelde waarde.sd is de standaardafwijking.Om een standaardnormaalverdeling te tekenen (gemiddelde = 0 en sd = 1), moeten we schrijven:
x <- seq(-10, 10, by = .1)
curve(dnorm(x, mean = 0, sd = 1), from=-4, to=4)
x <- seq(-10, 10, by = .1)Deze code maakt een reeks getallen tussen -10 en 10, oplopend met 0,1.
curve(dnorm(x, mean = 0, sd = 1), from=-4, to=4)Hiermee maken en plotten we een standaardnormale verdeling. We kunnen de grenzen handmatig instellen van -4 tot 4, zodat we inzoomen op het belangrijkste deel van de curve..
We kunnen verschillende soorten normale verdelingen weergeven. In het boek wordt gezegd dat cumulatieve SAT-scores bij benadering normaal verdeeld zijn met \(mu\) = 1100 en \(sigma\) = 200.
Om de normale verdeling van SAT-scores (gemiddelde = 1100 en sd = 200) uit te zetten, moeten we schrijven:
x <- seq(-10, 10, by = .1)
curve(dnorm(x, mean = 1100, sd = 200), from=200, to=2000)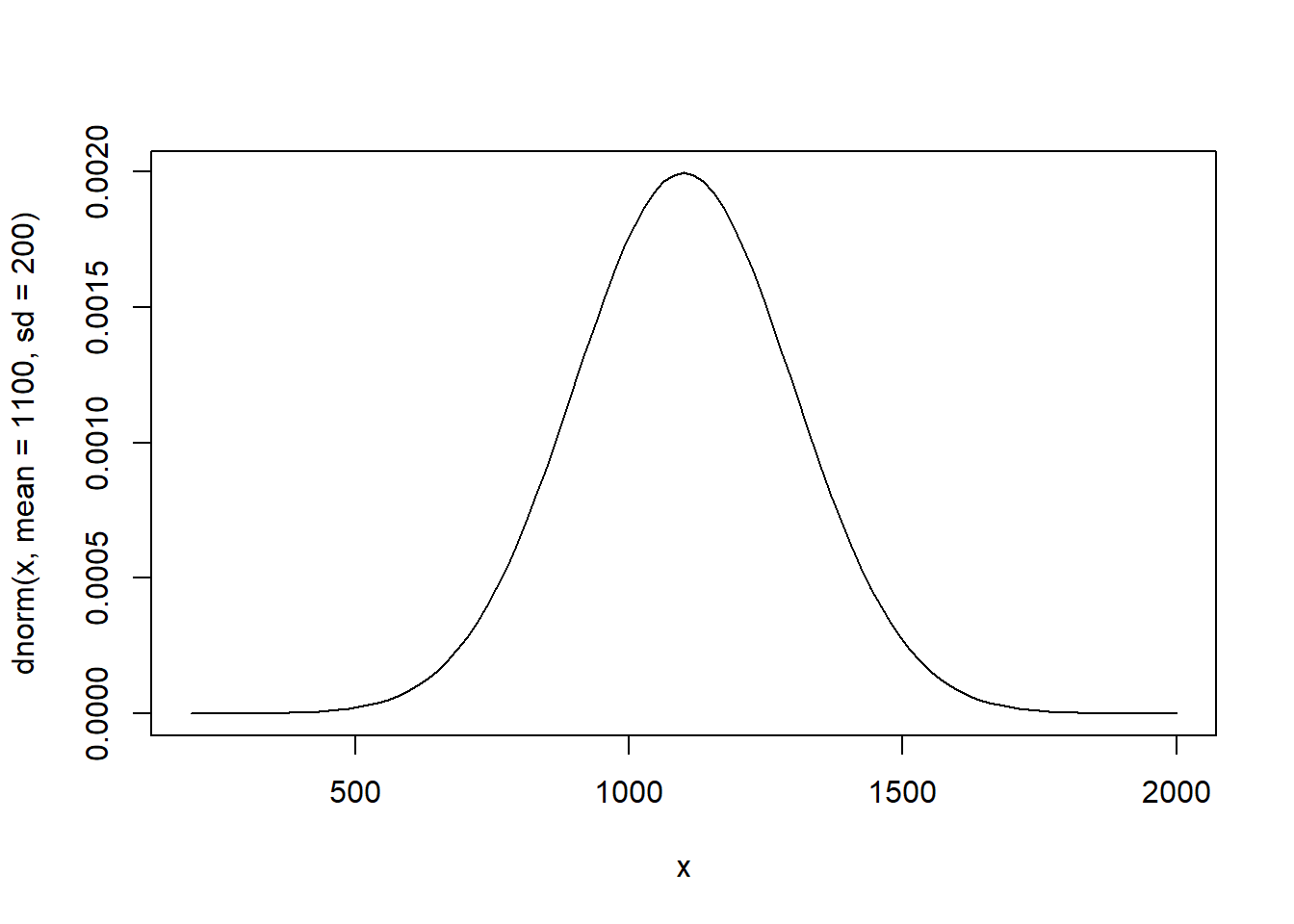
x <- seq(-10, 10, by = .1)Deze code maakt een reeks getallen tussen -10 en 10, oplopend met 0,1.
curve(dnorm(x, mean = 1100, sd = 200), from=200, to=2000)Hiermee maken en plotten we een normale verdeling met een gemiddelde van 1100 en een standaardafwijking van 200. We kunnen de grenzen handmatig instellen van 200 tot 2000, zodat we inzoomen op het belangrijkste deel van de curve.
De z-score is een maat die aangeeft hoe ver een bepaalde waarde in een bepaalde dataset onder of boven het gemiddelde ligt. De formule voor de z-score is:
\(z = \frac{x-\mu}\sigma\)
We gebruiken het voorbeeld van cumulatieve SAT-scores (\(mu\) = 1100 en \(sigma\) = 200) om de berekening van z-scores te illustreren. Om de z-score van een waarde van 1190 te berekenen, zouden we berekenen:
\(z = \frac{x-\mu}\sigma = \frac{1190-1100}{200}\)
(1190-1100)/200[1] 0.45Dit geeft aan dat de z-score positief is (0,45) en dat deze 0,45 standaarddeviaties boven het gemiddelde ligt.
Om het gebied in een standaardnormale (z) verdeling te vinden, kunnen we de functie pnorm() gebruiken. Maar let op: deze geeft standaard de oppervlakte, of waarschijnlijkheid, onder een bepaalde z-waarde (dus de linkerstaart (left tail)):
pnorm(0.45)[1] 0.6736448De waarde geeft dus aan dat 67,36 % van de waarden onder een z-waarde van 0,45 liggen. Als we geïnteresseerd zijn in het gebied boven een z-score van 0,45, dan is dat: 1 - 0.6736448 = 0.3263552. Dit kunnen we ook direct berekenen met pnorm door lower.tail = FALSE te specificeren:
pnorm(0.45, lower.tail = FALSE)[1] 0.3263552Ongeveer 32,65 % van de waarden ligt boven een SAT-score van 1190.
We kunnen ook het gebied tussen twee z-scores berekenen. Als we bijvoorbeeld geïnteresseerd zijn in het gebied tussen SAT-scores van 950 en 1200, berekenen we twee z-scores:
(950-1100)/200[1] -0.75(1200-1100)/200[1] 0.5De z-score van een SAT-score van 950 is - 0,75, de z-score van een SAT-score van 1200 is 0,5. Het gebied, of de waarschijnlijkheid, onder deze specifieke z-waarden (of, zo je wilt, van de linker staart) zijn:
pnorm(-0.75)[1] 0.2266274pnorm(0.5)[1] 0.6914625Vergeet niet dat beide de grootte van het gebied aan de linkerkant aangeven. Om de oppervlakte onder de curve tussen de twee SAT-scores te vinden, kunnen we dus de kleinste waarde (die overeenkomt met een SAT-score van 950) aftrekken van de grootste waarde. Dit geeft ons:
pnorm(0.5) - pnorm(-0.75)[1] 0.4648351Merk op dat we eenvoudigweg pnorm(0.5) - pnorm(-0.75) kunnen schrijven en R zal de waarde van pnorm(-0.75) (die 0.2266274 is) aftrekken van pnorm(0.5) (die 0.6914625 is).
Je kunt ook direct het gebied onder de curve berekenen zonder eerst de z-waarden te berekenen. Met de functie pnorm() kunnen we direct de waarde opgeven die we zoeken, samen met het gemiddelde en de standaardafwijking van onze normaalverdeling:
pnorm(1200, mean = 1100, sd = 200) - pnorm(950, mean = 1100, sd = 200)[1] 0.4648351Natuurlijk is het ook mogelijk om het omgekeerde te doen, bijvoorbeeld als we geïnteresseerd zijn welke SAT-score nodig is om tot de 10% beste scores te behoren. Hiervoor gebruiken we de functie qnorm(). Deze functie wordt standaard bij R geleverd en wordt gebruikt om de grenswaarde te vinden die een gebied bepaalt. Stel bijvoorbeeld dat je dat 90e percentiel wilt vinden van een normaalverdeling waarvan het gemiddelde 1100 en de standaardafwijking 200 is. Dan vraag je om:
qnorm(0.9, mean = 1100, sd = 200)[1] 1356.31qnorm(0.9, mean = 1100, sd = 200)Deze code berekent het punt onder de curve waar 90% van de leerlingen in een populatie die normaal verdeeld is met gemiddelde 1100 en standaardafwijking 200 onder zal liggen. Je kunt de waarden veranderen afhankelijk van de situatie. Als je het 45e percentiel van een normale verdeling wilt berekenen, schrijf dan qnorm(0.45, mean = 1100, sd = 200).
visualizeAls alternatief kunnen we het visualize package gebruiken om kansverdelingen grafisch weer te geven. Dit package is erg handig omdat we hiermee ook de gezochte waarde kunnen afbeelden.
library(visualize)Stel dat we het gebied onder de curve onder SAT-scores van 950 willen plotten bij een normaalverdeling van SAT-scores (gemiddelde = 1100 en sd = 200), dan moeten we schrijven:
visualize.norm(stat = 950,
mu = 1100,
sd = 200,
section = "lower")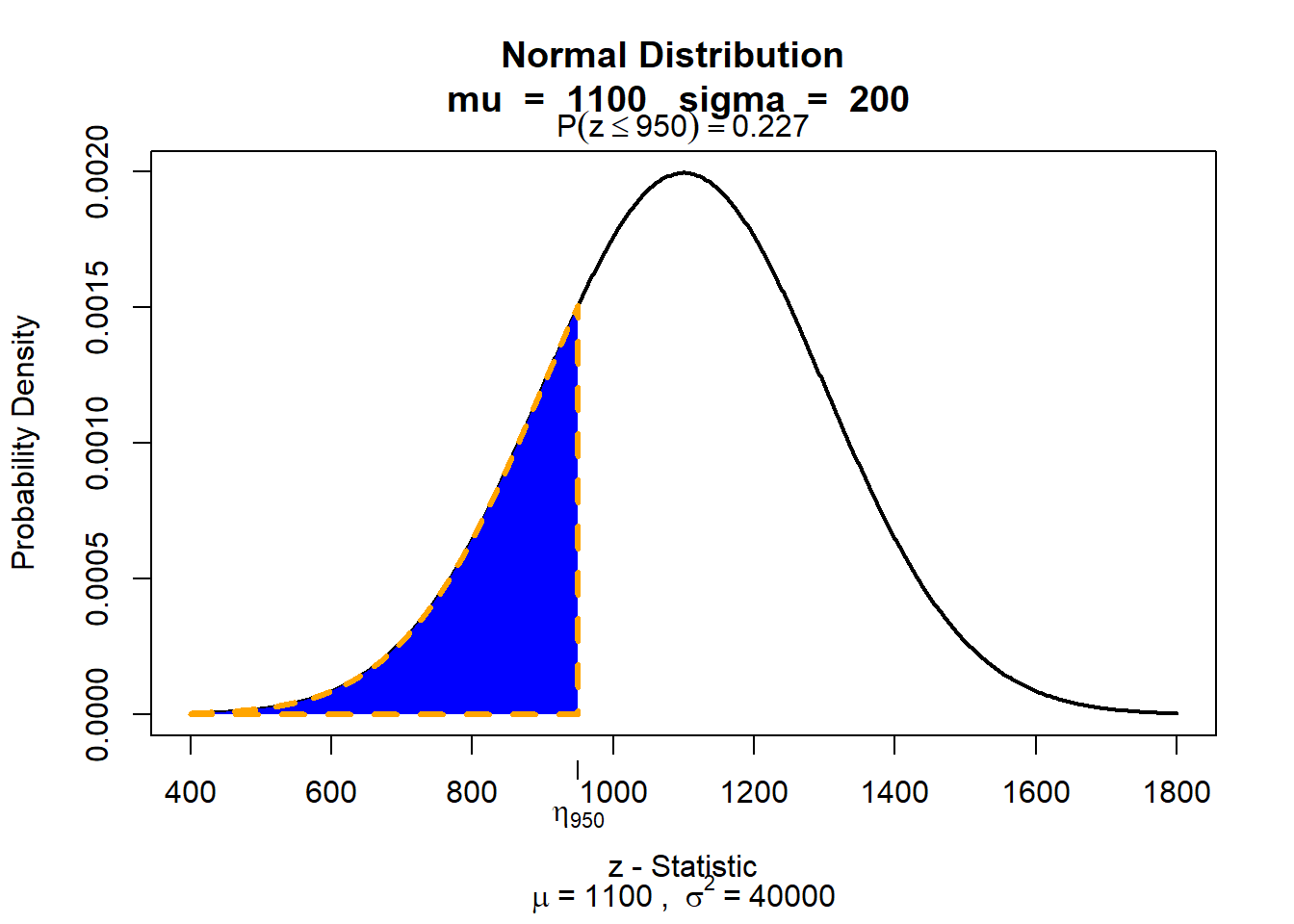
visualize.norm(...)visualize.norm() genereert een plot van de normaalverdeling met door de gebruiker opgegeven parameters.
stat = 950Hier geven we de grenswaarde op (in dit voorbeeld een SAT-score van 950).
mu = 1100Dit specificeert het gemiddelde van de normaalverdeling.
sd = 200Dit specificeert de standaardafwijking van de normaalverdeling.
section = "lower"Hier kies je welk gebied je wilt arceren en berekenen. De opties zijn “lower” (gebied onder de grenswaarde), “upper” (gebied boven de grenswaarde), “bounded” (gebied tussen twee grenswaardes) en “tails” (de twee staarten van de verdeling).
Om de oppervlakte onder de curve tussen SAT-scores van 950 en 1200 in een normaalverdeling van SAT-scores (gemiddelde = 1100 en sd = 200) uit te zetten, moeten we schrijven:
visualize.norm(stat = c(950, 1200),
mu = 1100,
sd = 200,
section = "bounded")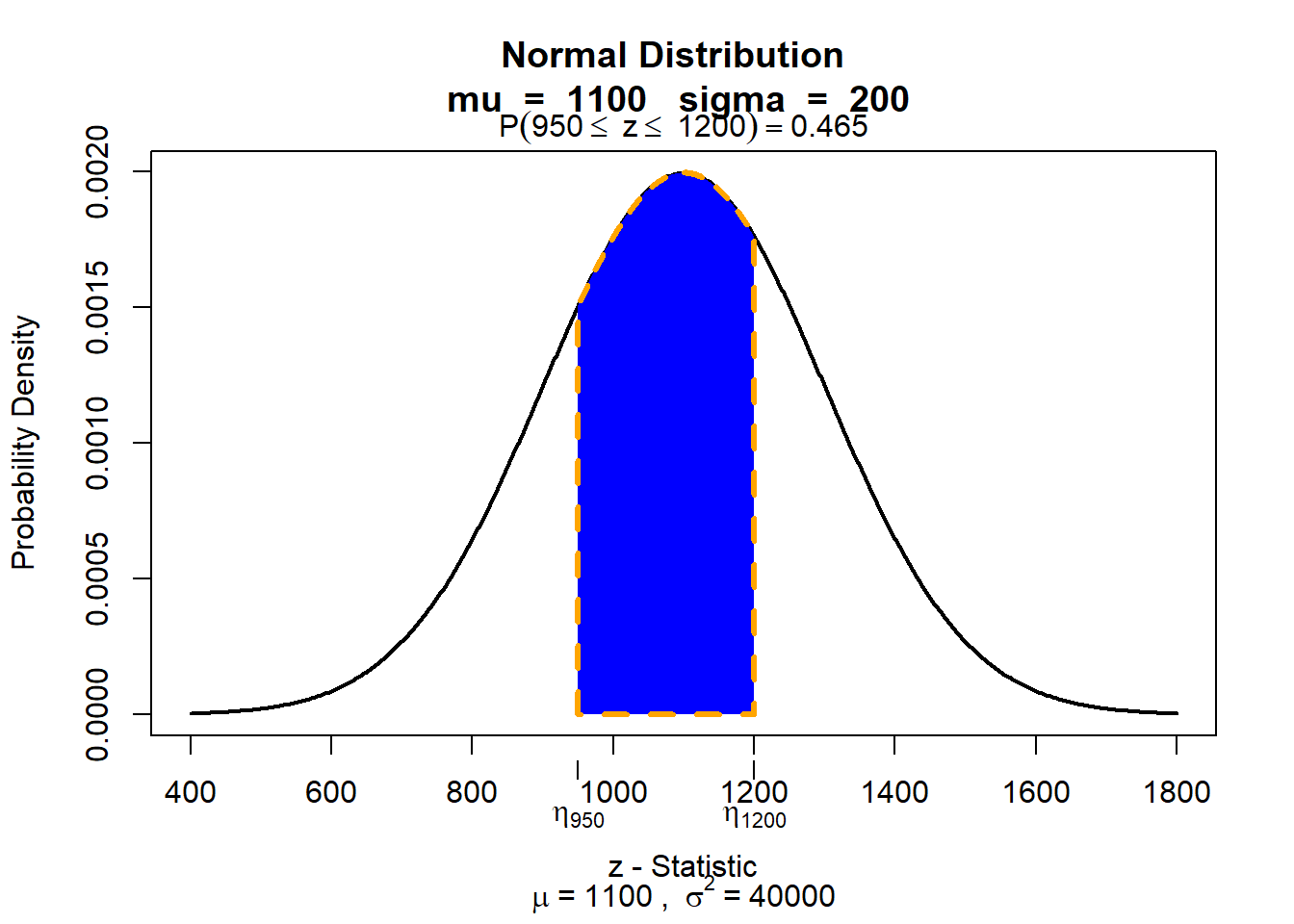
visualize.norm(...)visualize.norm() genereert een plot van de normaalverdeling met door de gebruiker opgegeven parameters.
stat = c(950, 1200)We willen de grootte van het gebied tussen twee punten berekenen, dus definiëren we stat = c(<ondergrens>, <bovengrens>).
mu = 1100Dit specificeert het gemiddelde van de normaalverdeling.
sd = 200Dit specificeert de standaardafwijking van de normaalverdeling.
section = "bounded"Hier kies je welk gebied je wilt arceren en berekenen. De opties zijn “lower” (gebied onder de grenswaarde), “upper” (gebied boven de grenswaarde), “bounded” (gebied tussen twee grenswaardes) en “tails” (de twee staarten van de verdeling).